三次元の回転(Exponential Map)
SLAMの論文を読んでいると三次元の回転表現としてExponential Mapを使った表現を用いているものが多くある。Exponential Mapを用いることで、回転行列や同時変換行列を加法的に閉じた空間へ写像することが可能になる。これにより、2点間の変換パラメータを線形に補間することが可能になる。この辺の話は、以下の文献に詳しく書かれている。
Lie Groups for 2D and 3D Transformations
Exponential Mapを用いた3次元回転群SO(3)は3次元ベクトルω(ベクトルの方向が回転軸、ノルムが回転量θ)を用いて以下のように表すことができる。
また、SO(3)のExponential Mapの逆変換であるLogarithm Mapは以下のように表される。
Exponential Mapを取り扱うことができるライブラリを探していたところ、C++のライブラリとしてSophusというものが比較的簡単に導入できそうなので試してみた。
Sophus
SophusはHeader Onlyのライブラリであり、依存しているのもEigenのみなので、SophusとEigenをinclude directoryに指定するだけで利用可能になる。以下は、3次元回転群SO(3)をSophusを用いて利用する例である。
Lie Groups for 2D and 3D Transformations
Exponential Mapを用いた3次元回転群SO(3)は3次元ベクトルω(ベクトルの方向が回転軸、ノルムが回転量θ)を用いて以下のように表すことができる。
また、SO(3)のExponential Mapの逆変換であるLogarithm Mapは以下のように表される。
Exponential Mapを取り扱うことができるライブラリを探していたところ、C++のライブラリとしてSophusというものが比較的簡単に導入できそうなので試してみた。
Sophus
SophusはHeader Onlyのライブラリであり、依存しているのもEigenのみなので、SophusとEigenをinclude directoryに指定するだけで利用可能になる。以下は、3次元回転群SO(3)をSophusを用いて利用する例である。
#include <iostream>
#include "sophus/geometry.hpp"
int main() {
// 単位行列
Sophus::SO3d R0;
std::cout << "R0:\n" << R0.matrix() << std::endl;
// x軸周りに180度回転
const double kPi = Sophus::Constants<double>::pi();
Sophus::Vector3d w(kPi, 0.0, 0.0);
Sophus::SO3d R_x_pi = Sophus::SO3d::exp(w);
std::cout << "R_x_pi:\n" << R_x_pi.matrix() << std::endl;
// クォータニオン [x, y, z, w]
std::cout << "クォータニオン(R1):\n"
<< R_x_pi.unit_quaternion().coeffs() << std::endl;
// 回転の合成
Sophus::SO3d R1 = Sophus::SO3d::rotX(kPi / 4); // x軸周りに45度回転
std::cout << "R1:\n" << R1.matrix() << std::endl;
std::cout << "R1*R_x_pi:\n"
<< (R1 * R_x_pi).matrix() << std::endl;
// ベクトルの回転
Eigen::Vector3d x;
x << 0.0, 0.0, 1.0;
std::cout << "x\n" << x << std::endl;
std::cout << "R1*x\n" << R1 * x << std::endl;
return 0;
}
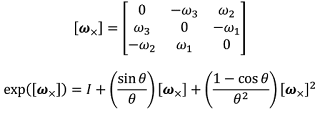

コメント
コメントを投稿